/*
-- Title : t-test 검정 예제
-- Reference : BDMBA, datacenter 김O지 임O총
-- Tag : t-검정 t test t 검정 등분산 양측 검정 우측 검정 좌측 검정 f검정 f-test f-검정
*/
양측검정
· H_0: 같다
· H_1: 다르다
우측검정(greater)
· H_0: 같다
· H_1: 차이가 0보다 크다
좌측검정(less)
· H_0: 같다
· H_1: 차이가 0보다 작다

양측 검정이 단측 검정보다 위험도가 낮다. 위 사진에서 볼 수 있듯이, 기각역이 양측 검정이 단측 검정보다 끝 쪽에 있기 때문에 H_0를 채택할 확률이 높아진다. 그렇기 때문에 양측 검정은 H_0를 채택하고자 할 때 (즉, 두 값이 같음을 보이고자 할 때) 사용한다. 반면에 단측 검정은 H_1을 채택하고자 할 때 (즉, 한쪽 값이 더 크다는 것을 보이고자 할 때) 사용한다.
예시-1)
"Ad study" data present pre-exposure and post-exposure attitude scores from an advertising study involving 10 respondents. Examine whether advertising increased the mean attitude score. Which test should we use: paired or independent sample t-test?
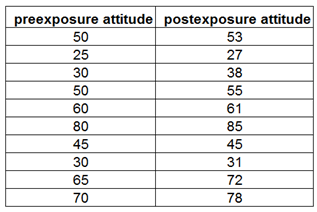
위의 표본은 한 집단에 대한 전후를 비교하므로 paired smaple t-test를 진행한다.
이전 평균이 50.5, 이후 평균이 54.5이므로 평균이 증가했기 때문에 광고의 효과가 있음을 검증하자.
광고의 효과가 있다는 것은, 이후 태도 점수가 더 높다는 뜻이기 때문에 좌측검정(차이가 0보다 작다)을 수행한다.
이전 태도 점수 = x, 이후 태도 점수 = y라 하면, 귀무가설과 대립가설은 다음과 같다.
H_0: x = y (변화가 없다.)
H_1: x - y < 0 (증가한다.)

>> paired t-test의 결과, p값이 유의수준(0.05)보다 작기 때문에 H_0를 기각한다. 즉, H_1을 채택하기 때문에 광고의 효과가 있다고 주장할 수 있다.
예시-2)
You want to compare the prices by two supermarket chains—Miller’s and Albert’s. Using a standardized one-week shopping plan (grocery list), you made identical purchases at 10 of each chain stores. The stores are randomly selected and all purchases are made during a single week. Examine whether the mean weekly expense at Miller’s is different from that at and Albert’s. Which test should we use: paired or independent sample t-test?
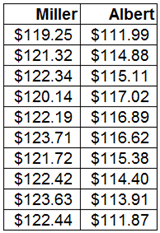
위의 표본은 두 집단에 대한 값을 비교하므로 independent sample t-test를 진행한다.
Miller의 평균은 121.92, Albert의 평균은 114.81이므로 Miller의 상품과 Albert의 상품의 가격이 다르다고 주장할 수 있음을 검증하자.
Miller의 상품과 Albert의 상품의 가격이 다름을 검정해야 하기 때문에 양측검정(같지 않다)을 수행한다.
Miller의 상품 가격 = m, Albert의 상품 가격 = a라 하자.
independent sample t-test이기 때문에 두 집간의 등분산성을 먼저 테스트 해야 한다.
(1) 이를 위해 f-test를 진행한다.
H_0: 등분산
H_1: 이분산

>> f-test의 결과, p값이 유의수준(0.05)보다 크기 때문에 H_0를 채택한다. 즉, 두 집단은 등분산임을 주장할 수 있다.
(2) 이제 이분산 t-test를 진행한다.
H_0: m = a (상품의 가격이 동일하다.)
H_1: m ≠ a (상품의 가격이 다르다.)
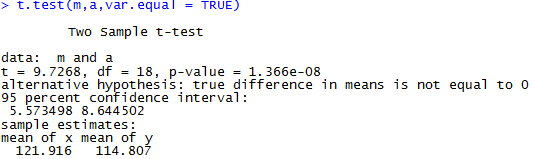
>> paired t-test의 결과, p값이 유의수준(0.05)보다 작기 때문에 H_0를 기각한다. 즉, H_1을 채택하기 때문에 Miller의 상품과 Albert의 상품의 가격이 다르다고 주장할 수 있다.